Adversarial Attack P1-Basic Conception

Adversarial Attack 要讲这个主题,我们这边要讲的是,我们在作业裡面,我们已经训练了非常多,各式各样的类神经网路,那我们当然期待说,我们可以把这些技术用在真正的应用上

但是光是把这些 Network 用在真正的应用上,要把这些 Network 用在真正应用上,光是它们正确率高是不够的,它们还需要什麼能力呢

他们需要能够应付来自人类的恶意,有时候你的 Network,它的工作是為了要侦测一些有恶意的行為,如果今天它的工作是要侦测有恶意的行為,这些它要侦测的对象,会去想办法骗过 Network,Network 在一般的情况下,都可以得到高的正确率是不够的,它要在有人试图想要欺骗它的情况下,也得到高的正确率

举例来说 我们今天都会用 Network,来做 E-Mail 的 Filtering,你会用 Network 来做侦测一封邮件,它是不是垃圾邮件,那今天对於一个垃圾邮件的发信者而言,他也会想尽办法避免,他的邮件被分类為垃圾邮件,如果今天有人他想办法去更改邮件的内容,想要去欺骗过 Network 的话,那 Network 到底能不能不要被欺骗呢

所以今天我们希望我们的类神经网路,它光是正确率高还不够,我们希望它可以应付来自人类的恶意

举例来说 这个是蚁王

牠叫做梅路艾姆,牠是站在生物顶点,牠是生物顶点的一个存在,牠非常地强,人类没有办法打赢牠,那牠会消灭掉所有的人类,但是人类并没有跟牠打,人类是不讲武德的,人类就直接放一个核弹就把牠炸死,然后故事就结束了 就这样

Example of Attack

我们先来看一个真正的例子,我们今天在好多个作业裡面,我们都已经训练了影像辨识的模型,也就是说你有一个影像辨识的系统,给它一张照片,它可以告诉我们说,这张照片属於什麼样的类别

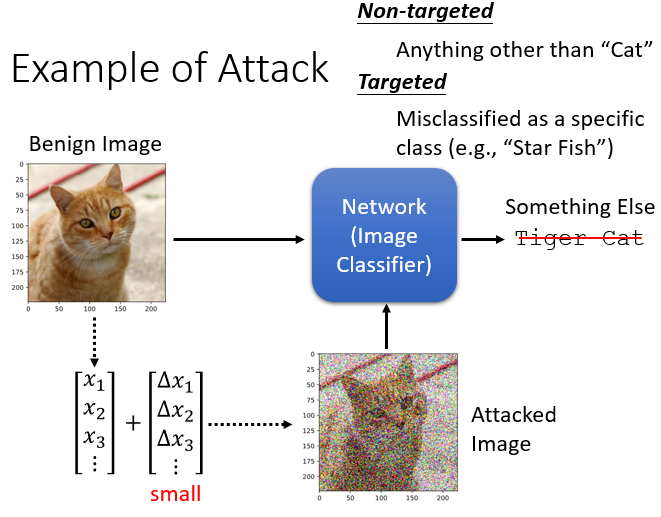
那今天我们要做的事情是,在这张照片上面加入一个非常小的杂讯,一张照片可以被看作是一个非常长的向量,我们在这个非常长的向量上加入,每一个维度都加入一个小小的杂讯,把这个有加入杂讯以后的照片丢到 Network,看看会发生什麼样的事情

那一般这个杂讯都非常非常地小,小到什麼地步呢,最好小到人肉眼没有办法看出来,所以这个例子裡面加的杂讯其实太大了,一般这个杂讯是小到人肉眼看不出来的

有被加杂讯的照片叫做 Attacked Image,有被攻击的照片,那还没有被加杂讯的照片呢,我们一般就叫做 Benign Image,它是好的 Image,它是还没有被攻击的图片

Benign Image 丢到 Network 裡面,它的输出是猫,那我们期待说 Attacked Image,就我们现在是攻击方 我们是坏人,我们希望 Attacked Image 丢到 Network 裡面,它的输出不可以是猫,要变成其他的东西

那攻击呢 大致上可以分成两种类型,一种是没有目标的攻击,没有目标的攻击是,原来的答案是猫,只要你能够让 Network 的输出不是猫,你就算是成功了

但是还有另外一种更困难的攻击,是有目标的攻击,也就是说我们希望 Network,不止它输出不能是猫,还要输出别的东西,比如说 我们希望加了一个杂讯以后,Network 输出呢 是海星,它把猫错误判断成一隻海星,才算是攻击成功,好 那这样子的攻击真的有可能做到吗,我们真的可以加入一个人肉眼看不到的杂讯,去改变 Network 的输出吗

实际上是可以的,这边用的 Network 并不是一个很弱的 Network,它是 50 层的 ResNet

当我们把一个 Benign Image 没有被攻击的图片,丢到 50 层的 ResNet 的时候,它的输出是 Tiger Cat

你知道今天这种影像辨识的系统,它的输出都不只会告诉你它是什麼动物,还会告诉你它是哪一个品种的动物,所以它给它这隻猫,它不只说它是 Cat,还说它是 Tiger Cat,不过据说这个答案其实是错的,据说这个猫不是 Tiger Cat,不过没有关係,反正它都认得出这个是一隻猫就对了,至少知道是一个猫科的动物

那它还有一个信心的分数,信心的分数(置信度)是 0.64,这个信心的分数是什麼呢,这个信心的分数就是,做完那个 Soft Mask 以后,得到的那个分数,就假设你的影像分类的类别有 2000 类,2000 个类别都会有一个分数,那这个分数呢 一定介於 0 到 1 之间,而且 2000 个类别的分数合起来,会刚刚好是 1

那既然有 2000 个类别那麼多,Tiger Cat 可以拿到 0.64 的分数,那其实算是挺高的

接下来呢 我们在这个 Benign Image 上面,加入一些杂讯,我们现在希望成功攻击的目标,是把 Tiger Cat 变成海星,而被攻击以后的图片长的是这个样子的,你可能问说 杂讯加在哪裡呢,杂讯已经加进去了,但它非常非常地小,小到人的肉眼根本没有办法看出来

把这张图片丢到 ResNet 以后,会发生什麼事呢,ResNet 的 Output 变成 Star Fish,而且它的信心分数是 100 % 啊,本来它还没有那麼确定这是不是一隻猫,现在它百分之百确定,它就是海星

那為了要证明说,这两张照片还是有一些不一样的,我们把它做一下相减

光做相减是不够的,做完相减以后,还要把它们的差距放大 50 倍,你会得到这样子的结论,所以这两张照片确实有些不一样,我并不是把同一张照片复製两次来骗你,它们是有一点不一样的,但是人根本看不出,这点不一样会造成什麼样的影响,但是对 ResNet 而言,它却有了天差地远的输出

那也许有人会觉得说,啊 也许是因為猫跟海星有什麼特别的关係

我们可以把猫变成海星只是一个特例,这不是一个特例,你可以把这隻猫轻易地变成任何的东西,我完全可以加上另外一个杂讯,就让这隻猫变成一个键盘,它一样信心分数高达 0.98,本来不太确定它是不是猫,现在加入另外一个杂讯以后,Network 98% 确定它就是一个键盘

那有人可能会觉得说,欸 怎麼会发生这麼离谱的行為,会不会是这个 Network 太烂了？,我要告诉你 它可是有 50 层的喔,它可不是一个非常烂的 Network

如果你加入的只是一般的杂讯,它并不一定会犯错,这个是原来的图片,我们现在加入一个杂讯,这个杂讯是你肉眼可见的

• 你可以很明显地看到,这张图片裡面被加入了杂讯,这个时候 ResNet 觉得,它看到的是 Tabby Cat,这可能才是正确答案,但无论如何 它都知道是猫科动物

• 把杂讯加得更大一点,它说这是 Persian Cat 这是波斯猫,可能杂讯加得大一点,这个猫看起来毛茸茸的,所以 ResNet 觉得它看到了波斯猫

• 把杂讯再加更大一点,你可能已经不知道这是什麼东西了,这个时候 ResNet 说,它看到了 Fire Screen,Fire Screen 是什麼呢,我 Google 了一下发现,Fire Screen 长这个样子,这裡完全可以理解机器為什麼会犯错,它觉得前面的杂讯是这个屏风,而后面这个橙色的猫就是火焰

它虽然犯错 它错的是有尊严的,它错的是有道理的,但不知道為什麼,加入一个人肉眼看不到的杂讯的时候,它却產生了天差地远的结果

How to Attack

那接下来我们在讲為什麼这件事会发生之前,我们来看看刚才所说的攻击,究竟是如何做到的,我们到底是怎麼加入了一个非常微小的杂讯,可以让 Network 產生非常错误的结果呢

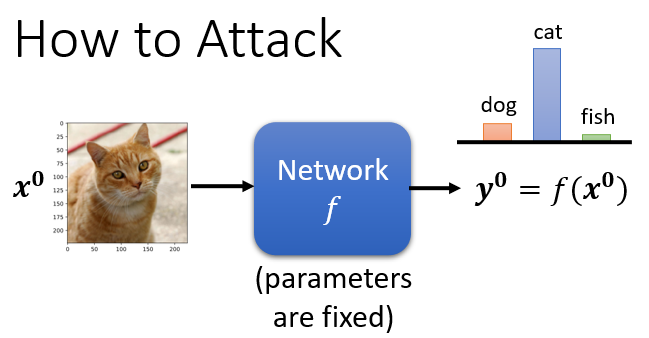
而这个是我们的 Network,它是一个 Function 我们叫它 f,这个 Function 输入是一张图片,我们叫它 $x^0$,它的输出是一个 Distribution,这个是这个分类的结果,那我们叫它 $y^0$

那我们这边假设 Network 的参数就是固定的,我们不讨论 Network 的参数的部分,Network 的参数不是我们今天的重点,所以它是固定的

• 如果是 Non-Targeted Attack 的话,我们要怎麼找出 Non-Targeted Attack 的杂讯呢

  我们现在要做的目标就是,我们要找到一张新的图片

  

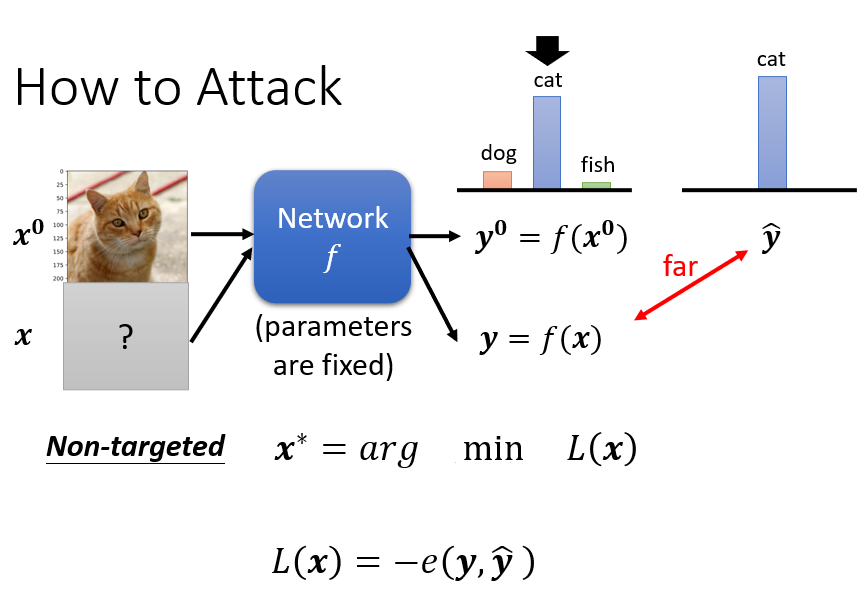
  这张新的图片呢 我们用 x 来表示,当我们把 x 丢到这个 Network f 的时候,它的输出是 y,我们正确的答案叫做 ŷ,我们希望 y 跟 ŷ 它的差距越大越好

  那怎麼做到这件事呢,怎麼找到这个 x,丢到一个 Network 裡以后,它產生的 y 跟 ŷ 差距越大越好呢？

  我们一样要解一个 Optimization 的问题,这个跟我们训练的 Network,其实是非常类似的

  我们先定一个 Loss Function,这个 Loss Function 呢,叫做 L,这个 L 呢 是 y 跟 ŷ 之间的差距,取一个负号,举例来说,我们一般在做这个 Classification 的时候,我们训练的目标 y 跟 ŷ,都是看它的 Cross Entropy,那我们这个 -e(y, ŷ),这一项代表的就是 y 跟 ŷ 之间的 Cross Entropy

  但是我们希望这个 Cross Entropy 越大越好,所以我们今天在 Cross Entropy 前面加一个负号,那这个负的 Cross Entropy 就是我们的 Loss,而我们期望这个 Loss 越小越好,我们希望找到一个 x,x 可以让 L(x) 越小越好,L(x) 越小 就代表说 y 跟 ŷ,它们的 Cross Entropy 越大,也就是 y 跟 ŷ 它们的距离越大,这个是没有目标的攻击

• 如果是有目标的攻击的话

  

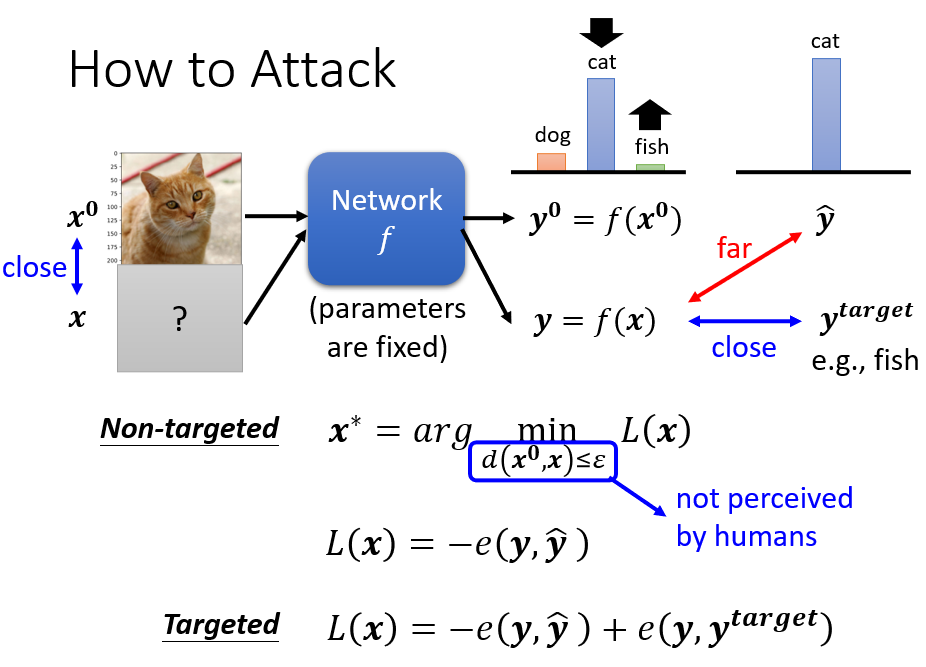
  那我们会先设定好我们的目标,我们用 $y^{target}$ 来代表我们的目标,那 ŷ 其实是一个 One-Hot Vector,$y^{target}$ 也是一个 One-Hot Vector,那我们现在希望这个 y 不止跟 ŷ 越远越好,我们还要跟 $y^{target}$ 越近越好

  所以假设你的 $y^{target}$​ 是一个 Fish,那你希望你输出的这个 y 啊,它不止 Cat 的机率越低越好,Fish 的机率还要越高越好,那你的 Loss Function 就写成这样

  $$L(\mathbf{x})=-e(\mathbf{y},\mathbf{y}\hat{})+e(\mathbf{y},{\mathbf{y}}^{\mathbf{target}})$$

  我们的 Loss Function

  • 是负的 y 跟 ŷ 之间的 Cross Entropy,希望这一项越大越好
  • 同时你又希望 y 跟 $y^{target}$,它们越小越好
  • 你把这两项加起来就是你的 Loss,你希望找一个 x,去 Minimize 这个 Loss

  但光是找一个 x,去 Minimize Loss 是不够的,因為我们其实还期待说,我们加入的杂讯越小越好,也就是我们新找到的图片,可以欺骗过 Network 的图片,跟原来的图片要越相近越好,x 跟 $x^0$ 要越近越好

  所以我们在解这个,Optimization 的 Problem 的时候,我们还会多加入一个限制,这个限制是

  $$d(x^0,x)\le \epsilon$$

  它的意思就是,我们希望 x 跟 $x^0$ 之间的差距,小於某一个 Threshold,小於某一个閾值,那这个閾值是根据什麼东西来决定的呢,通常就是根据人类的感知能力来决定

  如果 $x^0$ 跟 x 之间的差距大於 Σ,我们假设人就会看到这个杂讯,人就会发现有一个杂讯存在,所以我们要让 $x^0$ 跟 x 它的差距,小於等於 Σ,小於等於人类可以感知的极限,那我们就可以產生一张图片,人类看起来 x 跟 $x^0$ 是一模一样的,但產生的结果对 Network 来说,是非常不一样的

好 那怎麼计算 x 跟 $x^0$​ 之间的差距,它们之间的距离呢?d($x^0$​,x) 就代表它们之间的距离

有各式各样不同的算法,那為了等一下符号的方便起见呢,我们假设 x 是一个向量,因為它是个图片 所以它是个向量嘛,$x^0$​​ 是另外一张图片,它也是一个向量,这两个向量相减 我们叫它 Δx ./images/image-20210810231653104.png

那这个距离啊

• 你可以定 L2-Norm 当做它们的距离,也就是说你可以计算 Δx 的 L2-Norm,Δx 的 L2-Norm 就是把这个 Δx 的第一位,拿出来取平方,第二位拿出来取平方,第三位拿出来取平方,在这边你其实要开根号也可以啦,就看你的 L2-Norm 的定义是怎样,你要开根号也是可以的
• 另外还有一个定义呢 是 L-Infinity,L-Infinity 是怎麼看的呢,它就是把这个 Δx 拿来,然后看裡面哪一个维度它的绝对值最大,那这一个就是L-Infinity,就把 Δx1 Δx2 Δx3,也就是 Δx 的每一维都拿出来取绝对值,看谁最大,最大的那一个就代表 x 跟 $x^0$​​ 之间的距离

那有各种不同的方法,可以计算两张图片之间的距离,但是我们在决定要使用哪一种方法,来计算图片的距离的时候,其实我们应该把人类的感知把它考虑进来

那 L2 跟 L-Infinity 到底哪一个,在 Attack 的时候是比较好的距离呢,以下我举一个例子来跟大家说明

这是一张图片,假设这个图片只有四个 Pixel 而已,现在啊,我们把这张图片做两种不同的变化

第一个变化是这四个 Pixel 的顏色,都做了非常小的改变 ./images/image-20210810232148760.png

第二种变化是只有右下角这个 Pixel,它的顏色被改了,而且改的是比较大的 ./images/image-20210810232209129.png

如果我们今天在计算 L2 的 Norm 的时候,上面这两张图片的 L2-Norm,和下面这两张图片的 L2-Norm 是一样的 ./images/image-20210810232311223.png

这两个变化他们的 L2 的 Norm 是一样的

而但是如果你看 L-Infinity 的话,它们是不一样的,因為 L-Infinity 只在意最大的变化量,那对於 L-Infinity 而言,下面这个改变它最大的变化量是比较大的,上面这个改变最大的变化量是比较小

那如果从这个例子来看 L-Infinity 跟 L2,哪一个比较接近人类的感知能力呢,也许应该是 L-Infinity 吧

因為对你来说,其实这两张图片,我相信多数人你可能都看不出,它们之间有什麼差别,那我跟你保证它们两个之间是有差别的,就它们是有非常非常微小的差别,只是它的差别是分布在每一个 Pixel 上面

而这下面这两个改变呢,你会很明显的看到右下角这个绿色,它的顏色变深了,虽然这另外这三个 Pixel 的顏色是固定的,右下角的顏色一变深,你就发现有图片有变化,就发现这个图片有做到,有做了某种修改,所以看起来 L-Infinity 也许更符合实际的需求,我们要避免被人类,我们要避免被人类发现

光是 L2 小是不够的,我们要让 L-Infinity 小才是最好的,才是比较不会被发现,所以在作业裡面我们是用 L-Infinity,来当做我们的限制,来当做攻击,那我们作业就是要去攻击一个,JudgeBoi 上面的那个,像辨识系统產生出来的图片,我们会有所限制说,新的图片跟旧的图片,跟原来 Benign 图片的差距,要小於某一个 Threshold,那我们在定这个差距的时候,我们就是选择 L-Infinity,那实际上这个差距要怎麼定才是比较好,这个也要凭 Domain Knowledge

我们刚才举的例子是影像上的例子,如果我们今天要攻击的对象,其实是一个跟语音相关的系统,我们的 x 跟 $x^0$​​ 其实都是声音讯号,那什麼样的声音讯号,对人类来说听起来有差距,那就不见得是 L2 跟 L-Infinity 了,你就要去研究人类的听觉系统,看看人类对什麼频态的变化特别敏感,那根据人类的听觉系统来制定,比较适合的 x 跟 $x^0$​​ 之间距离的衡量方式,那这个部分就是需要用到 Domain Knowledge

Attack Approach

好 那我们现在已经有了,我们的 Optimization 的问题,我们要做的事情就是,我们要去 Minimize 是一个 Loss,那现在我们要找一个 x 去 Minimize 这个 Loss,但是这个 x 我们是有限制的 ./images/image-20210810232828937.png

x 跟 $x^0$​​ 它们的 Distance 要小於等於 x,那这个问题到底要怎麼解呢,我们先把这个限制拿掉

如果把这个限制拿掉,你会不会解这个问题呢,你其实会解这个问题,因為这跟我们 Train 一个模型其实没有什麼差别啊,我们在第一堂课的时候,就列过这个 Optimization 的问题给你看,告诉你说你可以调你的 Network 的参数,去让一个 Loss 最小

我们今天只是把参数改成Network 的 Input 而已 ./images/image-20210810233009320.png

你就把 Input 那一张 Image,看作是 Network 参数的一部分,然后 Minimize 你的 Loss Function 就结束了

现在 Network 的参数是固定的,我们只去调 Input 部分,让 Input 的部分去改变,去 Minimum 一个 Loss 就结束了,用的一样是 Gradient Descent,怎麼做呢

你就这样做啦,就是你要先有个 Initialization 嘛,我们现在找的对象不是 Network 参数,是 x,是你 Input 的 Image,但是它还是需要一个初始化的值 对不对

你还是需要一个,做 Gradient Descent 的时候初始化的值,那初始化的值设什麼样的数值比较好呢

• 你可能不会从随机的 Image 开始,你可能会从 $x^0$​​ 开始,因為我们本来就希望说,我们新找到的 x 应该跟 $x^0$​​ 越接近越好嘛,那你何不就从 $x^0$​​ 开始找呢,你从 $x^0$​​ 开始找
• 你接下来找出来的 x 可能就会跟 $x^0$​​ 比较接近,所以你初始化的 x,你会初始化的这个 $x^0$​​ 就直接设 $x^0$​​,然后接下来就跟,一般的 Gradient Descent 是一模一样的,我们就是 Iterative 去 Update 你的参数,你就设一个 Iteration,t 等於 1 到 T,然后在每一个 Iteration 裡面,你都会计算 Gradient,只是这个 Gradient 不是 Network 参数,对 Loss 的 Gradient,我们现在已经不管 Network 参数了,而是 Input 那一张 Image x,对於 Loss 的 Gradient,那 Input 这个 x,它也是一个很长的向量嘛,它裡面就是有 x1 x2 x3 嘛,你就去计算这个 Input Image 裡面,每一个数值对 L 的偏微分,就 x1 对 L 的偏微分,x2 对 L 的偏微分,算出来,算出一个 Gradient,用这个 Gradient,去 Update 你的 Image 就结束了
• 所以你本来的 Image $x^0$​​​​,它就减掉这个 Gradient,那前面你也会乘上一个 Learning Rate,就跟一般 Gradient Descent 是一模一样的,只是要做 Gradient Descent 的对象,从参数换成 Input 而已,其他都是一样的,也有 Learning Rate 那些什麼东西统统都有,乘上一个 Gradient,乘上 Learning Rate,减掉原来的 Image,然后就得到新的 Image,你可以 Iteration 地跑,就跟一般的 Gradient Descent 是一模一样

但是这个是在没有 Constraint 的前提,接下来我们得把 Constraint 加进去

因為一般我们在做 Gradient Descent 的时候,我们并没有把那个,Gradient Descent 的对象做什麼限制,我们并没有设限说,我们的参数一定要长什麼样子

那现在我们是有限制的,我们限制说 x 跟 $x^0$​​,他们的差距一定要小於等於 $x^0$​​,那要怎麼处理这个问题呢

你就在你的 Gradient Descent 裡面,再加一个 Module ./images/image-20210810234123458.png

这个我们要跑 Gradient Descent 这个演算法,但是我们要同时考虑 $x^0$​​ 跟 x 之间的差距,怎麼考虑这件事情呢,这边呢,这个方法说穿了不值钱,非常地简单

你 Update 完你的参数以后发现,你的 $x^t$ 跟 $x^0$​​ 的差距大於 ε 以后,你就做一个修改,把 $x^t$​ 做个修改,把它改回符合限制就结束了

举例来说,假设我们现在用的是 L-Infinity,我们的这个 $x^0$​​ 在这个地方,那我们的 x 它可以存在的范围,就只有这个方形框框的范围 ./images/image-20210810234321048.png

因為 L-Infinity 是考虑 $x^0$​​ 跟 x 之间最大的差距,所以出了这个框架的差距就会超过 ε

所以今天呢你在做完这个 Gradient Descent,用 Gradient 去 Update 你的 x 以后,它一定还是得要落在这个框框裡面才行,那怎麼保证 Update 以后,一定落在这个框框裡面呢,你就,只要 Update 超出了框框,就把它拉回来就结束了

所以今天这个步骤如果做完,你发现你得到蓝色这个点跑出框框了怎麼办,在框框裡面找一个跟蓝色的点最近的位置,把蓝色的点拉进来就结束了,就结束了

那其实这种 Attack 有非常多不同的变形,我想你在文献上可以找到,各式各样的 Attack 方法,但其实它们的精神都不脱,我们今天讲的这个事情,那它们通常不一样的地方都是,要嘛是 Constraint 不一样,要嘛是 Optimization 的方法不一样,但是通常都还是用 Gradient Descent,它们的精神还是一样的,只是这边你可能会有不同的 Optimizer,这边你可能会有不同的限制,它就变成不同的 Attack 方法,但它们精神都不脱,我们今天跟大家举的这个例子

好 那接下来呢,我们跟大家介绍一个最简单的 Attack 的方法,也是作业裡面你要过Simple Baseline 所用的方法,

这个 FGSM 它是怎麼做的呢,非常地简单,它叫做 Fast Gradient Sign Method 缩写 ./images/image-20210810235052519.png

它怎麼做呢,它就像是一个一拳超人一样,它只用一击,本来一般你在做 Gradient Descent 的时候,你要 Update 参数很多次,但是 FGSM 它厉害的地方就是,它决定只 Update 一次参数,看看能不能够一击必杀,一击就找出一个可以 Attack 成功的 Image,所以首先呢,本来要 Iterative 的去 Update 参数,但是现在不用,我们只做一次的攻击,我们只做一次的 Attack

然后 G 这边呢,它做了一个特别的设计,那至於為什麼做这个特别设计,大家再去看一下原始文献,可以了解当初為什麼会有这样的想法,它说我们不要直接用这个,Gradient Descent 的值,我们给它取一个 Sign ./images/image-20210810235129202.png

这个 Sign 是什麼意思,这个 Sign 的意思是说,如果括号裡面的值大於 0,我们就输出 1,括号裡面的值小於 0,我们就输出 -1,所以加了 Sign 以后,这个 g 这个 Vector 啊,它裡面要嘛是 1 要嘛是 -1 ./images/image-20210810235200844.png

本来如果你是算 Gradient,它的值可以是任何的 Real Number,但现在取 Sign,它要嘛是 1 要嘛是 -1,所以 g 裡面就都是 1 或者是 -1,然后 Learning Rate 呢,Learning Rate 就设 ε,就看你这边的这个 ε 设多大,这边 Learning Rate 直接设一个一模一样的,直接设个一模一样的会得到什麼效果呢 ./images/image-20210810235304739.png

会得到的效果就是,你攻击完以后,你一定落在这个蓝色框框的四个角落的地方,因為你想想看哦,这个 G 它要嘛是 1 要嘛是 -1,它每一维要嘛是 1 要嘛是-1,那前面会乘上 ε,所以乘完 ε 以后,你今天的 $x^0$​​,要嘛就是往右边移 ε,要嘛就是往左边移 ε,要嘛就是往上移 ε,要嘛就是往下移 ε,

所以今天做完一次攻击以后,你的这个 $x^0$​​ 做完一次攻击以后,它一定会挪到这个四方形的四个角落的地方,它一定是这四个角落的其中一个,那光做这件事,光做这个一击往往就可以必杀,所以这个你可以过 Simple Baseline

那有同学就会问说一击必杀有什麼好呢,如果我多攻击几次,多跑几个 Iteration 结果不会更好吗,会更好,所以多跑几个 Iteration,就过 Medium Baseline 就这样子 ./images/image-20210810235432175.png

所以怎麼多跑几个 Iteration,你就把本来是只跑一个 Iteration 啊,现在就多跑几个 Iteration 啊,几个 Iteration,你要跑几个 Iteration,高兴都是你自己设,就设个比如说 3 啊 5 啊 10 啊,多跑几个 Iteration

那但是多跑几个 Iteration 的坏处是,你有可能一不小心就出界,有可能一不小心就跑出了这个四方形的范围,那跑出四方形的范围后怎麼处理呢,非常简单,把它拉回来就结束了,你就看说在这,如果这个蓝色的点 Update 以后,跑出这个四方形,你就看这四个角落,哪一个角落跟蓝色的点最近,就选那个角落,就结束了,好 这个就是 Iterative 的 FGSM,它可以帮你过 Medium 的 Baseline